A* (AStern) Algorithmus

In keinem Studium zur Spieleprogrammierung darf der A* (A Stern) Algorithmus fehlen. Auch ich durfte diesen in einem C++ Beispiel visualisiert mit der Clanlib Engine umsetzen. Alles was ihr zum AStern Algorithmus wissen müsst und wie man diesen in C++ implementiert.

A* (A Stern) Algorithmus

In jedem Computerspiel ist eine gute Wegfindung notwendig. Ob nun Panzer über eine 2D Karte fahren oder die KI Gegner im aktuellen Shooter über eine 3D Karte laufen. Ohne gute Wegfindung bleiben die Gegner stecken, laufen oder fahren unnatürliche Wege oder noch schlimmer: bewegen sich gar nicht. Der A* Algorithmus ist eine Möglichkeit diese Wegfindung umzusetzen.

Funktionsweise

Der A* Algorithmus wird am besten über das Gif auf der Wikipedia Seite visuell erklärt. Der Algorithmus versucht über den direkten Weg (Luftlinie) das Ziel zu erreichen. Feld für Feld werden Knoten mit allen Nachbarn in einem Graphen angelegt. Bricht dieser Versuch durch ein Hindernis ab, dann werden die Nachbarn der erzeugten Knoten vom Start weg verwendet und so weiter. Jeder Knoten der bereits besucht wurde wird nicht erneut besucht. Je komplexer die Hindernisse desto mehr Felder müssen im Graphen angelegt werden, im schlimmsten Fall (es gibt keinen Weg) alle Felder die erreichbar sind.

Über eine Heuristik werden alle Knoten bewertet. Im einfachsten Fall ist das der Abstand zum Ziel, ich verwende die Manhattan-Metrik. Dabei zählt man die Entfernung zum Ziel als direkten Weg. Im Gif werden diese Werte in den Farben rot (weit weg) bis grün (am Ziel) dargestellt. Nachdem der erste Pfad das Ziel erreicht wird der Graph Knoten für Knoten zurück vom Ziel zum Start durchgegangen. Bei mehreren Nachbarn wird jeweils das Feld genommen mit dem niedrigsten Wert der Metrik. Voila, wir haben den Pfad mit den geringsten Kosten gefunden und brauchen den Rest der Karte nicht absuchen.

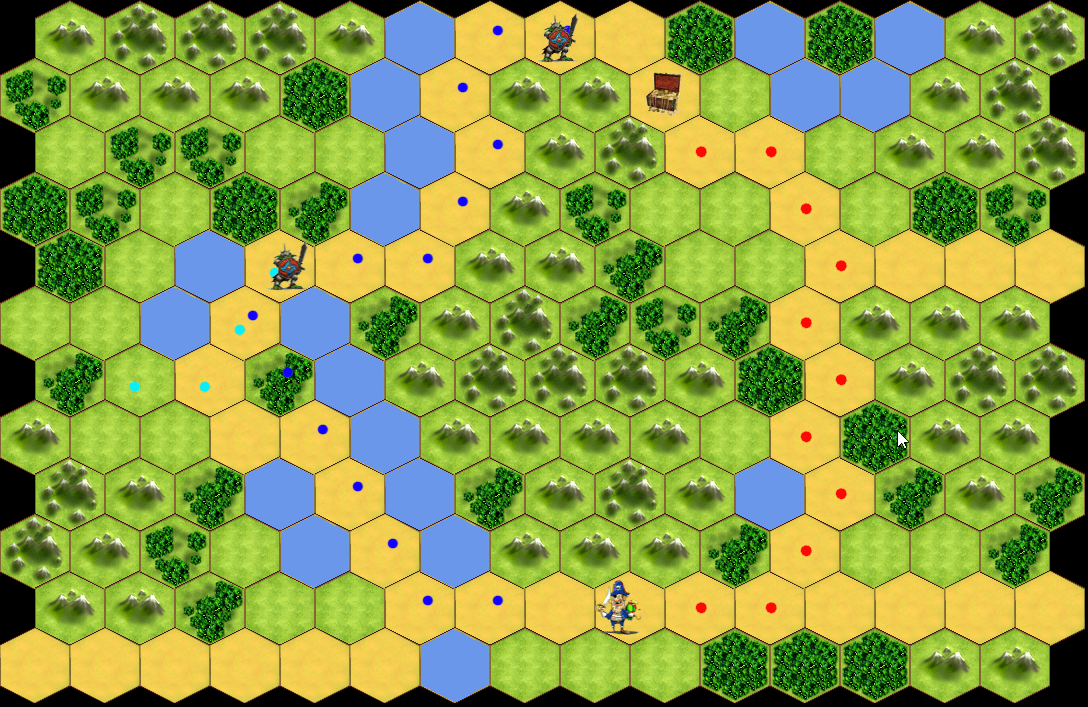
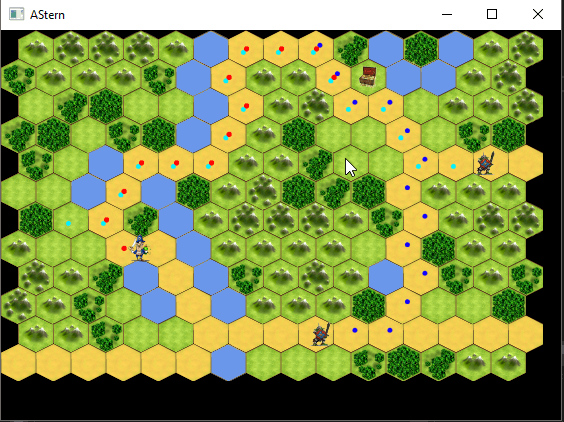
Der A* Algorithmus findet so nicht nur einen Weg zum Ziel, er feindet den schnellsten Weg (der Weg mit den geringsten Kosten). Definiert man pro Feld unterschiedliche Kosten (Weg = geringe Kosten, Wald oder Berge = hohe Kosten), dann findet die Spielfigur einen Weg der auf dem visualisierten Weg der Spielgrafik liegt und läuft eher ungern durchs Gebüsch.

In meinem Beispiel habe ich den AStern Algorithmus mit Feldern unterschiedlicher Kosten implementiert. Damit das noch dynamischer wird verändern patrouillierende Gegner diese Kosten, der Held berechnet den Pfad laufend neu und weicht im Notfall aus.

Implementierung

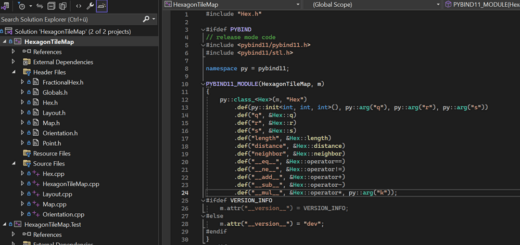
Den vollständigen Source Code findet man wie immer auf meiner GitHub Seite. Aufgrund der Komplexität des Programms verweise ich auf die Kommentare im Code und auf meine vorangegangenen Artikel zum Waldbrand, Damenproblem, Lindenmayer Systeme, Sanduhr und 4 Gewinnt. Dort ist schon alles bezüglich verwendeter Klassen und Arbeit mit der ClanLib dokumentiert.

Der AStern Algorithmus ist in der AStar Klasse implementiert (astar.h) und wird über folgende Methoden gesteuert:

• init
  initialisiert den Algorithmus mit den Parametern start und ziel (Koordinaten von wo bis wo ein Pfad gesucht werden soll). Mit dem dritten Parameter legen wir fest ob es sich um einen Pfad des Gegners handelt.
• searchPath
  der eigentlich AStern Algorithmus in einer Schleife ausprogrammiert
• getPath
  liefert den gefundenen Pfad als Pointer auf den Startknoten und der Länge (Anzahl der Knoten = Felder)

Aufgerufen wird diese Berechnung in der App::createPath Methode. Besonders interessant ist die searchPath Methode. Dort wird in einer Schleife so lange gesucht, bis alle Knoten geprüft wurden oder ein gefundener Pfad diese Berechnung früher abbricht. Abbruchbedingung ist eine Prüfung, ab der aktuell zu bearbeitender Knoten das Ziel ist. Falls nicht holt man alle Nachbarn und fügt diese in der expandNode der todo Liste von Knoten hinzu. Das sind all jene Felder der Karte, die in diesem Durchlauf noch nicht besucht wurden. Besonders interessant ist nun die pathCostEstimate Methode, die für jeden neuen Knoten die Kosten berechnet. Die searchPath nimmt für den nächsten Durchlauf jenen Knoten in der todo Liste mit dem kleinsten Kostenwert (der dem Zeil am nächsten ist). Sollten irgendwann alle besuchbare Knoten besucht worden, dann liefert expandNode keine neuen Knoten in der todo. Dort werden alle abgearbeiteten Knoten entfernt. In diesem Zustand hat der Algorithmus festgestellt: es gibt keine Lösung.

Gegner

Der in der init Methode definierte boolsche Wert für einen Gegner legt fest, dass in der getCost Methode zusätzlich noch eine Potentialmap für die Kostenrechnung eingebaut wird. Das ist eine zweite Karte auf der numerisch nicht der Typ gespeichert wird (der Typ legt fest ob ein Weg, Wald, Berg oder Wasser gezeichnet wird), sondern dort werden um den Gegner herum die Nachbarfelder mit numerischen Werten besetzt. Diese multiplizieren den ursprünglichen Wert der Wegsuche, das bedeutet diese Felder haben einen drastisch höheren Kostenwert. Bei der Pfadberechnung werden die fast immer ignoriert (Ausnahme: es gibt keinen anderen Weg).

Hexagon oder quadratische Felder

Eine wichtige Designentscheidung bei der Darstellung ist die Form der Felder. Ich habe mich für Hexagone (Sechsecke) entschieden. Das hat einen für den A* Algorithmus einfachen Grund. Jedes der 6 Nachbarfelder ist gleich weit entfernt. Bei quadratischen Feldern hingegen gibt es zwei Möglichkeiten:

• 4 Nachbarn mit gleicher Entfernung
  ein Feld hat einen Nachbarn rechts, links, oben und unten. Die Wegstrecke (die Entfernung) ist jeweils gleich.
• 8 Nachbarn, wobei die diagonalen Felder anders bewertet werden können oder auch nicht
  • diagonale Felder haben gleichen Abstand wie horizontale bzw. vertikale Felder
    das führt zum Problem, dass der Pfad tendenziell eher über die Diagonalen verläuft und unnatürlich wirkt.
  • diagonale Felder haben einen anderen Abstand
    die Qualität des Ergebnisses hängt vom definierten Abstand ab. Ein möglicher Wert wäre die Wurzel aus 2 (also ca. 1,4)

Ihr seht, dass quadratische Felder gleich mal recht kompliziert werden, weshalb Hexagonale Felder schon seit langer Zeit bei 2D Spielen sehr beliebt sind (man denke an Panzer General, Battle Isle oder ähnliche Spiele).

Sonstiges

Neben den in meinen anderen Artikeln schon verwendeten Klassen sticht vor allem GameObject heraus. Von dieser Klasse erben andere Objekte wie das EnemyObject und das ist alles was auf der Karte gerendert wird und nicht die Karte selbst ist. Das sind die Gegner, die Pfadmarkierungen, der Spieler und sein Ziel. Die Implementierung ist recht trivial und sollte selbsterklärend sein.

In der globals.h findet man zahlreiche Parameter mit denen man herumspielen kann. Ich habe in diesem Beispiel mit unterschiedlichen Kartengrößen experimentiert, so schaltet man mit SMALL zwischen einer großen und kleinen Karte um.

Fazit

Der AStern ist ein effizienter und einfach umzusetzender Wegfindungs-Algorithmus. Besonders einfach gestaltet sich die Implementierung für eine 2D Karte. Dank einfacher Heuristik lassen sich sehr schnell sehr dynamische Berechnungen erstellen, der Charakter berechnet den Weg nicht nur aufgrund statischer topografischer Daten, sondern kann auch Gegner erkennen und darauf reagieren.