Terrain Rendering mit Geometrie Clipmaps für Spiele
heute möchte ich ein wenig Werbung in eigener Sache machen. Da meine Diplomarbeit wie ich finde sehr gut geworden ist hab ich beschlossen diese auch als Buch zu veröffentlichen. Hier eine Rezension über mein eigenes Buch.
Rezension
In diesem Buch geht es um das Erzeugen und Darstellen von Landschaften mit der Grafikkarte. Im speziellen geht es um das Rendern (zeichnen) der Landschaften mit einer relativ neuen Technik namens Geometrie Clipmaps.
Das Buch ist dabei in 3 Bereiche eingeteilt:
- Erzeugen von realistischen Landschaftsdaten
Hier zeige ich wie man unterschiedliche Landschaftstypen mit Algorithmen automatisch erzeugen kann. Darüber hinaus erkläre ich wie man diese Landschaften realistischer macht. - Darstellen von Landschaftsdaten mit den Clipmaps
Das ist ein sehr technisches Kapitel in dem genau beschrieben wird, wie man Geometrie Clipmaps auf der CPU und der GPU berechnet und welche Probleme auftreten können. - Analyse Spiele-Algorithmen
Im letzten Teil analysiere ich inwieweit Algorithmen, die oft in Spielen eingesetzt werden, mit den Clipmaps funktionieren.
Die zahlreichen Grafiken und Illustrationen demonstrieren dem Leser dabei sehr gut die Materie. Eingefügte Codebeispiele erklären dann noch wichtige Aspekte der beschriebenen Algorithmen. Der beigefügte Sourcecode ermöglicht dann jedem interessierten Leser selber mit dem Geometrie Clipmaps zu arbeiten.
Leseprobe
3.1.2 Diamond Square Algorithmus
Der Diamond Square Algorithmus ist dem Midpoint Displacement Algorithmus sehr ähnlich und wird deshalb auch oft als Random Midpoint Displacement Fractal bezeichnet. Er ist eine Erweiterung des Triangle Division Algorithmus, wobei hier die neu erzeugten Punkte abhängig von vier anderen Punkten anstatt von zwei berechnet werden.
Mit dem Gewichtungsparameter r kann man die Flachheit beziehungsweise die Grobheit des Terrains einstellen. Unterteilt ist der Algorithmus in einen Diamond und einen Square Schritt. Beim Diamond Schritt wird aus einer quadratischen Struktur eine Diamantstruktur erzeugt, im Square Schritt genau umgekehrt.
Der Algorithmus im Detail [20], siehe Abbildung 3.3:
- Man beginnt mit einem Viereck. Jeder Eckpunkt bekommt eine zufällige Höhe.
- Diamond Schritt: erzeuge einen Punkt in der Mitte der 4 Eckpunkte des Quadrats. Der Höhenwert ergibt sich aus dem Mittelwert der Eckpunkte plus einem Zufallswert.
- Square Schritt: erzeuge einen Punkt in der Mitte der 4 Eckpunkte des Diamanten. Der Höhenwert errechnet sich wie im Diamond Schritt.
- Nun wiederholt man Schritt 2 und 3 bis zum gewünschten Detailgrad.
Auch hier kann der Bereich der Zufallswerte frei gewählt werden, ein möglicher Wert wäre zum Beispiel zwischen -ri und ri. i startet mit dem Wert 1 und wird mit jedem Durchgang um eins erhöht, r ist der Gewichtungsparameter. Im Unterschied zum Triangle Division Algorithmus erhöht ein höherer Wert von r die Grobheit des Terrains.
Der Algorithmus liefert schon sehr realistische Terrains, jedoch können auch hier bei sehr flachen Terrains noch Artefakte sichtbar sein. Abhilfe schafft die Verwendung einer nicht linearen Interpolation der Eckpunkte zum Beispiel mit einer kubischen Spline Interpolation.
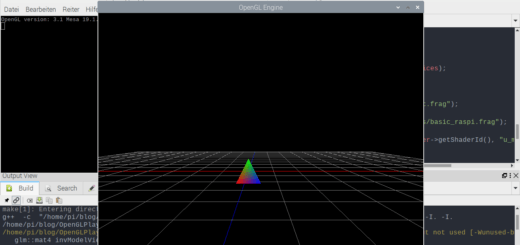
Beispielbilder
weitere Informationen
- Author: Werner Ziegelwanger
- Taschenbuch: 98 Seiten
- Verlag: Diplomica Verlag; Auflage: 1., Aufl. (30. November 2011)
- Sprache: Deutsch
- ISBN-10: 3842869959
- ISBN-13: 978-3842869950
- Größe und/oder Gewicht: 25,4 x 17,8 x 0,5 cm
Das Buch ist unter anderem auch bei Amazon erhältlich:
Terrain Rendering mit Geometrie Clipmaps für Spiele