Konvexe Hülle in C++

Das Beispiel konvexe Hülle in C++ stammt aus der Lehrveranstaltung Algorithmen und Datenstrukturen. In einem Fenster wird aus einer Summe von Punkten auf einer 2 dimensionalen Ebene eine konvexe Hülle um diese Menge gebildet. Effiziente Algorithmen zur Findung einer konvexen Hülle werden in zahlreichen Anwendungen benötigt.

Konvexe Hülle in C++

Gegeben ist eine Menge an Punkten. Gesucht ist eine Hülle, welche alle Punkte umschließt. Diese Hülle soll dabei eine möglichst kleine Fläche umschließen. Man spricht von einer konvexen Hülle (siehe dazu Wikipedia).  In diesem Programm kann man sich zufällige Punkte automatisch erstellen lassen oder eigene Punkte manuell setzen. Mit einem Tastendruck wird der Algorithmus zur konvexen Hülle ausgeführt und diese gezeichnet. Man kann diesen Algorithmus auch schrittweise durchgehen und zusehen, wie er Linie um Linie erzeugt. Setzt man danach neue Punkte wird die Hülle neu errechnet.

Implementierung

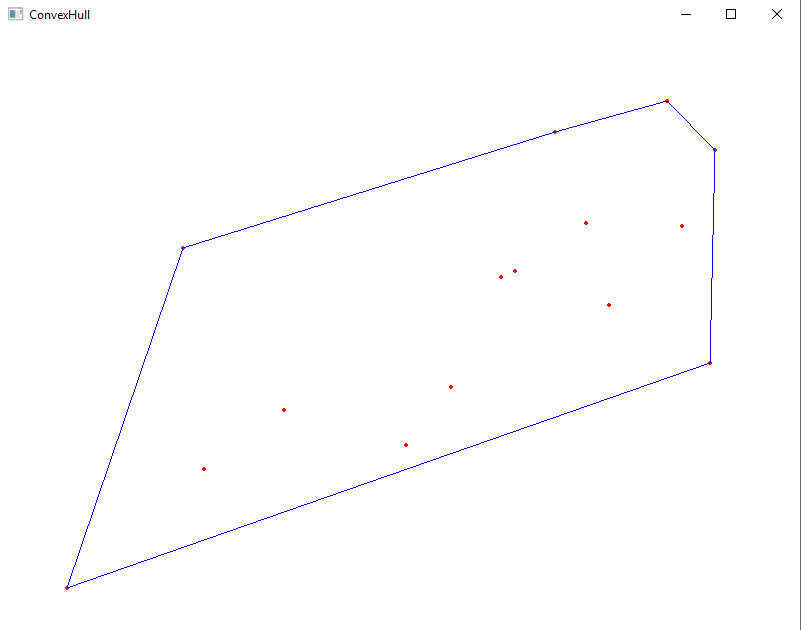
Wie immer findet man den Source Code für dieses Beispiel auf meiner GitHub Seite. Die grafische Darstellung ist mit der ClanLib Engine implementiert. Die grafische Ausgabe zeichnet in einem Fenster mit weißem Hintergrund die Punkte in rot mit einer blauen konvexen Hülle.

In der Methode App::createRandomPoints(int count) werden count viele zufällige Punkte in der 2D Ebene erstellt. Das passiert nur im sichtbaren Bereich, also zwischen 0 und WINDOW_WIDTH beziehungsweise 0 und WINDOW_HEIGHT. Die Fenstergröße ist in der precomp.h Datei definiert und können dort beliebig verändert werden. Als Zufallszahlen Funktion wird die Implementierung der boost Library verwendet.

In der Methode App::calculateHull(int step) wird die konvexe Hülle vollständig erzeugt. In der ähnlichen Methode App::calculateHullStep() wird nur der nächste Schritt, also die nächste Linie erstellt. Diese ruft aber immer nur App::calculateHull() mit dem jeweils nächsten step auf. Der Algorithmus sucht einen Extremwert, von dem aus wir die restlichen Punkte der Hülle suchen, beispielsweise wie im Bild zu sehen jener Punkt mit dem größten Y Wert (0,0 ist links oben). Nun rechnen wir uns den Winkel der Geraden zu jedem Punkt in der Menge aus und nehmen jene Linie mir dem kleinsten Winkel. Liegen auf der Geraden mehrere Punkte, dann nimmt man jenen, der dem Startpunkt am nächsten liegt. In einer Schleife sucht man so lange weiter, bis man wieder am initialen Startpunkt angekommen ist.

void App::calculateHull(int in_step)
{
    // return if list is empty
    if (m_vPoints.size() == 0) return;

    // get maximal number of points
    int iMaxStep = in_step == 0 ? m_vPoints.size() : in_step;

    int index_minimum = 0;
    int index_maximum = 0;

    m_vHull.clear();

    int i = 0;

    // find min and max
    for (std::vector<Position2D>::iterator it = m_vPoints.begin();
         it != m_vPoints.end();
         ++it)
    {
        // it there are more points with same y values
        if ((*it)._y > m_vPoints[index_minimum]._y)
            index_minimum = i;
       if ((*it)._y == m_vPoints[index_minimum]._y)
           if ((*it)._x < m_vPoints[index_minimum]._x)
               index_minimum = i;

       if ((*it)._y < m_vPoints[index_maximum]._y)
           index_maximum = i;
       if ((*it)._y == m_vPoints[index_maximum]._y)
           if ((*it)._x > m_vPoints[index_maximum]._x)
               index_maximum = i;
       ++i;
    }

    // add min to hull
    m_vHull.push_back(m_vPoints[index_minimum]);

    // get min angle for all points and add to hull as long as we are at the min value
    Position2D achse(1, 0);
    int index = index_minimum; // next point to check
    int next_index;
    double length;
    double angle;

    int j = 0;
    for (; j < iMaxStep; ++j)
    {
        // initialize angle with max (2 * pi)
        angle = 2 * PI;
        length = 99999.0f;
        // compute angle for every point that is not this point
        for (unsigned int i = 0; i < m_vPoints.size(); ++i)
        {
            if (m_vPoints[i] != m_vPoints[index])
            {
                Position2D pos = m_vPoints[i] - m_vPoints[index];
                double a = pos.getAngle(achse);
                if (a < angle)
                {
                    angle = a;
                    length = pos.getLength();
                    next_index = i;
                }
                // if points are on line -> choose nearest one
                if (a == angle)
                {
                    if (pos.getLength() < length)
                    {
                        length = pos.getLength();
                        next_index = i;
                    }
                }
            }
        }
        index = next_index;
        // if we are at max value -> choose negative axis
        if (index == index_maximum)
            achse._x = -1;
        if (index == index_minimum)
            break;
        m_vHull.push_back(m_vPoints[index]);
    }

    // loop was interrupted before reaching iMaxStep
    // we found a hull
    if (j < iMaxStep) {
        m_vHull.push_back(m_vHull[0]);
    }
}

Fazit

Die konvexe Hülle ist die kleinste konvexe Menge aus einer Ausgangsmenge. Das lösen dieser Mathematischen Aufgabe ist ein recht einfaches 2D Beispiel, welches immer wieder in Software benötigt wird. Diesen Algorithmus effizient umzusetzen lohnt sich, wenn man über die konvexe Hülle effizientere Abfragen auf eine Menge von Punkten durchführen will. Beispielsweise um schnell zu prüfen ob ein 2D Objekt die Punktmenge schneidet. Bevor man jeden Punkt einzeln prüft ist ein schneller Bounding Box – konvexe Hülle Test hilfreich.